现代神经网络是一种非线性统计性数据建模工具。
1. 为什么需要激活函数?
- 激活函数可以给模型引入非线性的因素。
- 假若网络中全部是线性部件,那么线性的组合还是线性,与单独一个线性分类器无异。这样就做不到用非线性来逼近任意函数。
- 使用非线性激活函数 ,以便使网络更加强大,增加它的能力,使它可以学习复杂的事物。使用非线性激活函数,能够从输入输出之间生成非线性映射。
2. 损失函数的确定与损失计算
确定一个能表述label和预测值之间误差值的损失函数,然后尽可能的通过更新权重w来优化这个损失函数,以达到提高预测准确率的目的。
3. 梯度
所谓梯度其实就是一个偏导数向量,但是我们经常说的仍是x的梯度而不是x的偏导数(就是对x求偏导)。利用网络中所有运算都是可微(differentiable)的这一事实,计算损失相对于网络系数的梯度(gradient),然后向梯度的反方向改变系数,从而使损失降低。
4. 反向传播
作用:对损失函数优化,将损失值降到最低.
反向传播算法就是梯度下降的求导链式法则的应用。
简单的说,就是损失函数E对每一个权重参数wi求导,然后用这个求得的导数去更新wi自身,因为在神经网络的隐藏层和输出层中存在不止一个层次的权重wi,所以需要从输出层开始向前一层一层的求导,这就是为什么叫做反向传播的原因。
以w10为例,要更新w10,需要先求得E对w10的导数。
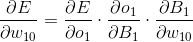
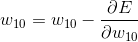
反向传播中,每一次迭代进行一次全体权重参数更新,直到参数不再更新,即得到全局最小值或局部最小值。
更新网络参数时,主要使用以下简单的更新规则:
weight = weight - learning_rate * gradient
什么时候进行反向传播?
一般是一个batch_size,一个batch算一次,可以让参数向着更加“正确”的方向前进,减少随机梯度下降带来的单样本随机抖动。
